Sound. What is sound? Learning sound. Sound waves. Fourier Sound Program.
Sound is a periodic, traveling compression and rarefaction (decreased density) of a substance. For example, if we could stop a sound wave traveling in air, we would find local variations in the air’s density.
These "increased air density packets" (compressions) travel away from the sound source at a constant speed. The regions of increased air density for a single pitch sound wave are always the same distance away from each other. This distance is called the wavelength. Frequency is the number of air compressions passing a location every second.
An important feature of sound waves (and waves in general) is that there is no net motion of the air molecules. Only the locations of the compressions and rarefactions move. Similar motion can be observed with a "slinky" around a meter stick. First tape the end coils of the "slinky" to the ends of the meter stick. Now compress a number of coils at one end of the meter stick and then suddenly release them. We observe a compression moving from one end of the meter stick to the other, but the coils themselves are just vibrating back and forth. Air molecules behave in a similar manner with respect to a sound wave. A region of increased air density moves through space, but individual air molecules vibrate back and forth over a small region as a result of the sound wave.
Consider walking by a car with the stereos’ volume and bass turned up to their limits. Can one perceive the sound without the use of one’s ears? How?
For the classic sci-fi movie "Alien", why did movie posters say "In space no one can hear you scream"? Note: the answer is more involved than one big scary monster with no one around for large distances.
Detection and production of sound waves
Imagine a series of sound wave compressions hitting a thin membrane as shown below.

When the sound wave collides with the membrane, the membrane will vibrate. By knowing how far the center of the membrane moves, one can measure the strength (amplitude) of the sound wave. By observing how many membrane oscillations occur in a second, one can determine the sound wave’s frequency. Microphones proportionally convert the membrane’s motion (distance traveled by the membrane’s center) into a voltage. Thus, by observing the voltage signal as a function of time, we can find the amplitude of the sound wave and its frequency.
Sounds waves are generated in a similar manner. A voltage signal is proportionally converted into a membrane’s motion (distance traveled by the membrane’s center). The membrane quickly pushes and pulls away from air molecules causing traveling compressions and rarefactions in air density. Hence, a sound wave is produced.
Fourier Sound Program
This program was designed to help students learn about sound waves as well as Fourier transform graphs. Upon opening the Fourier Sound program, the computer screen should look like:
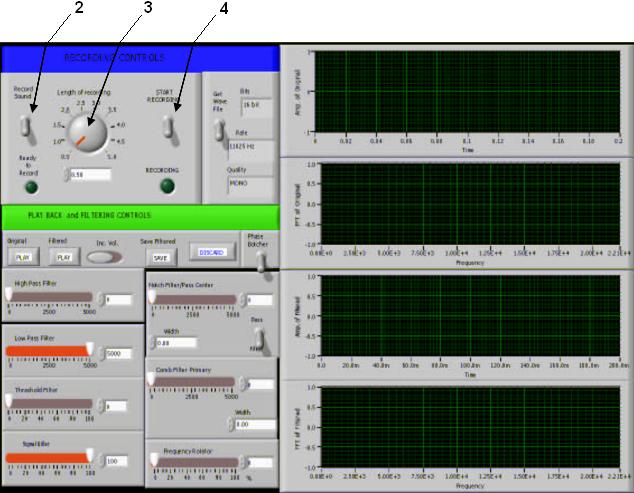
Recording a new sound
This set of instructions allows one to enter a recorded sound. As only one sound file can be adjusted at a time, you may need to delete the current sound file (if one was already entered). If this is the case, see the section called delete sound file.
- This requires you to attach a microphone to your computer’s sound card;
- Move the cursor (shaped like a small hand) to the switch in the upper left corner labeled "record sound"; NOTE: once this switch is thrown, you are now committed to record a sound; no other switches will be available; NOTE: the program will not record a sound until a second switch is thrown (see below);
- Now set the "length of recording" by moving the cursor over this dial (hold down left click and move mouse);
- Finally, move the mouse over the "START RECORDING" switch and left click.
Import a Wave file
This is an alternative method for entering a sound into the program (as opposed to recording a sound). As only one sound file can be adjusted at a time, you may need to delete the current sound file (if one was already entered). If this is the case, see the section called delete sound file.
- Move the cursor (shaped like a small hand) to the switch labeled "get wave file";
- A window should open allowing you to select the desired previously recorded sound file. NOTE: not all wave file formats will work.
- Move the cursor (shaped like a small hand) to the button labeled "discard" and left click (be patient for longer sound files);
- You will know that the sound has been discarded, when no curve appears on the graphs;
- If a toolbar appears over the red "RECORDING CONTROLS LABEL", you need to restart the program. This can be done in three ways:
- move the cursor over the menu: operate run;
- left click mouse on "run arrow";
- to prevent this problem from occurring again left click mouse on "continuous run arrow";
The below descriptions are for after you have entered a sound wave into the program (see either recording a new sound or importing a wave.
Original wave signal graphs (green traces):
- The microphone signal. That is, the values on the vertical axis describe the position of a thin membrane as a sound wave collides with it;
- Fourier transform of the signal.
- The modified microphone signal;
- Fourier transform of the modified sound wave.
Playing a sound wave:
- To hear the original sound wave, press the "original play" button;
- To hear the modified (filtered) sound wave, press the "filtered play" button.
- Left mouse click, the button labeled "SAVE"
All of these controls are adjusted by first moving the cursor over the desired control and then left click and hold while moving the mouse to adjust the slider.
- High pass filter – removes all musical pitches below a cut off value controlled by the slider;
- Low pass filter – removes all musical pitches above a cut off value controlled by the slider;
- Threshold filter – removes sound frequencies whose Fourier amplitude is below a percentage value of the maximum Fourier amplitude;
- Signal Killer - removes sound frequencies whose Fourier amplitude is above a percentage value of the maximum Fourier amplitude;
- Notch Filter/Pass – This control allows one to completely remove or only allow sound’s whose frequencies are within a range of values;
- Notch Filter/Pass center - allows one to change the center of the frequency window;
- Width – allows one to describe the size of the frequency window;
- Filter/Pass switch – If filter is selected sound frequencies in the described wave are removed. If pass, all sound frequencies outside the window are removed.
- Comb Filter – This filter allows you to remove a series of frequencies that are multiples of each other (i.e., remove 100 Hz, 200 Hz, 300 Hz, etc. sound frequencies);
- Comb Filter Primary – This control adjusts the lowest frequency to be removed;
- Width – This describes window width of the frequencies to be removed;
- Frequency Rotator – This control changes the frequencies of the recorded sounds;
- Phase Botcher Switch – The control will leave the Fourier transform unchanged. However, it changes (randomly) the phases between different sound frequencies.
- Record a simple sound wave by whistling into the microphone;
- Adjust the "Frequency Rotator". Then play the original sound and the filtered sound;
Use the Fourier transform graphs and your observations about the sounds to describe the relationship between musical pitch and frequency. How does frequency relate to musical pitch?; - Adjust the frequency rotator to zero and then throw the "Phase Botcher" switch. Play the filtered sound.
How does the phase botcher affect the sound? - Turn the "Phase Botcher" off. Discard the whistle sound, and record a person whistling with the sound of a tuning fork (you don’t have to match the musical pitch and its better if you don’t even try);
For each graph (microphone signal and Fourier transform), try to attribute which features are related to the whistle and which features are due to the tuning fork. Which recorded sound was louder, the whistle or the tuning fork? How can we determine this from the graphs? - Discard the whistle-tuning fork sound, and record a person singing a musical note.
How does a person’s voice compare to that of a whistle in terms of the microphone signal graph and the Fourier transform graph?
Imagine removing the largest frequency sound on the Fourier transform graph. Make a prediction of what this will do for the current sound (person singing). Make sure you explain your reasoning.
- Using the Notch filter/pass, remove the largest frequency from the current sound (person singing a note). Play the filtered sound;
How is the filtered sound different from the original sound? If there are any differences from your prediction (previous exercise), resolve them. - Turn the Notch filter/pass off (center frequency and width to zero). Now turn on the "Phase botcher". Play the filtered sound.
Describe the effect of the phase botcher on a person singing a musical note. How does this differ from when you used it on a whistle? Why is it different? - Turn off the phase botcher and discard the sound. Record the sound of a person speaking a sentence.
Make a prediction. If we removed the louder more prevalent sound frequencies, would you still be able to recognize the sentence when played back? If we removed the faintest frequencies, would you still be able to recognize the sentence when played back? Explain your reasoning. - Use the "Signal Killer" to remove the loudest frequencies in the Fourier transform graph and play the filtered sound wave. Try multiple settings.
How big of an effect was it when you removed the loudest frequencies from the sound wave? Did this match your prediction? If not, try to resolve the differences. - Use the "Threshold filter" to remove the faintest frequencies in the Fourier transform graph and play the filtered sound wave. Try multiple settings;
How big of an effect was it when you removed the faintest frequencies from the sound wave? Did this match your prediction? If not, try to resolve the differences: - Discard the sound and record a person whistling again with your lips close to the microphone;
- Play the sound wave (unaltered). Now using the appropriate filters, remove the blowing background sound from the whistle.
Comments: